|

|
|
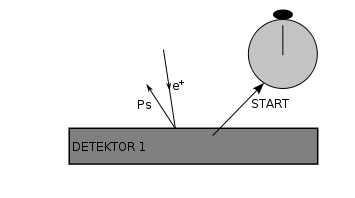
Figur 1.a: Positronen flyver ind i detektoren og starter stopuret. Samtidig kan positronen danne positronium. |
Figur 1.b: Positroniumatomet henfalder og udsender stråling, som opfanges af en anden detektor, som stopper tidstagningen. |

|

|
|
Figur 1.a: Positronen flyver ind i detektoren og starter stopuret. Samtidig kan positronen danne positronium. |
Figur 1.b: Positroniumatomet henfalder og udsender stråling, som opfanges af en anden detektor, som stopper tidstagningen. |
|
|
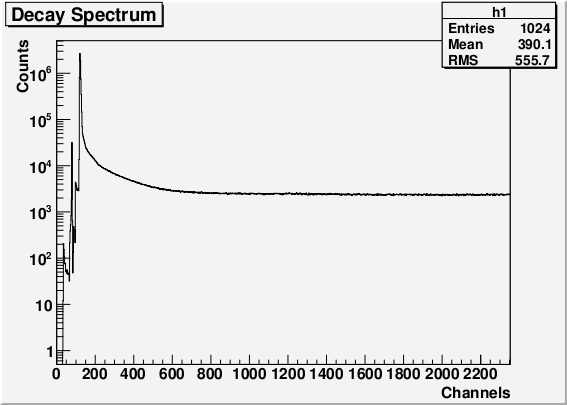
Figur 2: Et histogram over optagede levetider. Den tydelige top i venstre side af histogrammet stammer fra positroner, der annihilere med det samme, når de rammer detektoren. Den flade del i højre side af histogrammet er baggrundsstøj. Signalet fra positroniums levetid ligger imellem toppen og baggrunden. |
|
|
|
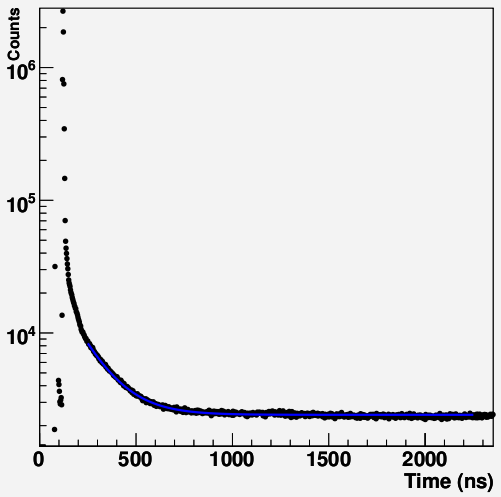
Figur 3.a: Den blå kurve er fittet til de sorte datapunkter. Når vi skal finde positroniums levetid, må vi starte med at fitte til hele intervallet, og gradvist gøre intervallet mindre, indtil vi finder der korrekte levetid. |
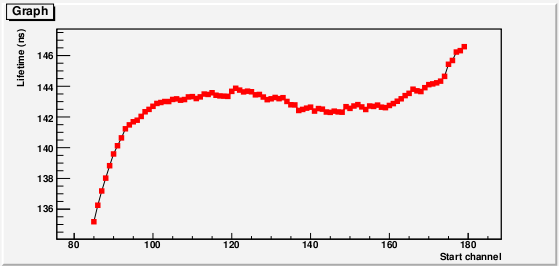
Figur 3.b: Levetiden som funktion af intervalstørrelsen. Når intervallet er for stort, bliver levetiden for kort, fordi noget af prompt-toppen er med i levetiden. Når intervallet bliver for småt, bliver levetiden for lang, fordi noget af baggrunden er med i levetiden. Der er et plateau imellem disse to ekstremer, som må være positroniums levetid. |

|
| Figur 4: Histogram over levetider. Levetiderne er vægtet med kvaliteten af fittet - dvs. dårlige fit har lavere værdi end gode fit. Den sorte kurve viser en normalfordeling, som er fittet til histogrammet. |